Slauncha

L'adaptation des populations naturelles vise à améliorer les chances de survie du groupe.

De leur côté, les modèles informatiques de l'évolution cherchent surtout à "engendrer" un individu dont le "code génétique" représente la solution optimale ou presque optimale d'un problème.

Mais pour accroître la probabilité qu'un tel événement se produise, le modèle doit peu à peu améliorer la qualité moyenne de "générations" entières de solutions potentielles, exactement comme c'est le cas pour la biologie.

Ci-après, nous donnons un exemple très simple de ce processus, reportant à plus tard une analyse détaillé du modèle. Cet article détaille la théorie ceux souhaitant mettre en pratique cette théorie, je vous invite à compléter votre lecture par cette article. Cet article détaille l'implémentation d'un algorithme génétique en Java.

Notre problème consiste à trouver un nombre entier x entre 0 et 127 pour lequel une fonction mystèrieuse f(x) - qui sera révélée plus tard - prends sa valeur maximale.
Chacun des nombres 0, 1, 2, ..., 126, 127 est une solution potentielle. Biologiquement parlant, ils sont les phénotypes (~ caractéristiques physiques d'un organisme) possible de l'espèce.
 

Remarque :

Pour ne pas compliquer l'exemple, nous avons restreint le nombre de solutions potentielles à quelques douzaines. Dans une situation réelle, où le nombre de possibilités serait astronomique, il est hors de question d'essayer de découvrir le maximum par le calcul systématique de toutes les valeurs de f(x) de la fonction.

On peut considérer la fonction f comme mesurant "l'adaptabilité" d'une solution potentielle x, à savoir comment x a réussi dans le "milieu". Plus grand est le score f(x), meilleure est la qualité du phénotype x. Notre but est alors de trouver un x dont l'adaptabilité est la plus grande possible.

La représentation graphique de f apparaît ci dessous. Comme c'est le cas pour n'importe qu'elle fonction d'adaptabilité, le graphe comporte plusieurs sommets et plusieurs creux.

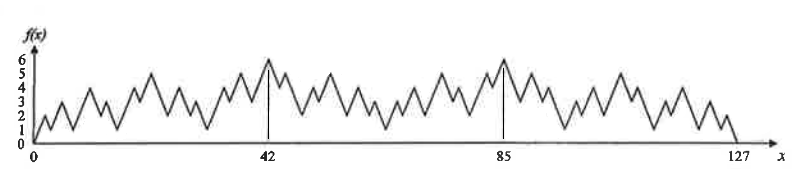
Le graphique d'une fonction mystérieuse.

Les plus hauts sommets correspondent aux meilleurs individus, c'est-à-dire aux solutions optimales.

Les autres sommets sont des maximums locaux, à savoir les meilleures solutions pour les valeurs x restreintes à un certain voisinage. Nous pouvons constater qu'il y a deux solutions optimales, x=42 et x=85.

Bien entendu, dans n'importe quel problème non banal le graphe de la fonction d'adaptabilité ne peut pas être tracé, et encore moins examiné, si bien que nous ne possédons aucun indice concernant l'identité des plus aptes ou dans quelle région les chercher.

Tout ce que nous pouvons faire, c'est tester les solutions individuelles par rapport à leur adaptabilité et utiliser au mieux cette information pour "engendrer" de meilleures solutions.

Dans ce qui suit, nous allons mettre en évident une méthode de résolution qui ne suppose aucune connaissance de f  autre que la possibilité de calculer les valeurs f(x) une à la fois.

La stratégie d'un algorithme génétique est basée sur les mécanismes de la sélection naturelle et de l'évolution. Sa mise en œuvre requiert normalement des ressources de calcul considérables pour stocker les données, automatiser les opérations et accélérer l'horloge évolutionniste. Après certaines étapes préliminaires (codage, sélection du pool de solution initial, etc), le plan évolutionniste procède de manière cyclique, pour produire une nouvelle "génération" de solutions potentielles après chaque cycle.

Une combinaison de hasard et de "reproduction" contrôlés favorisera à la longue l'apparition d'excellentes solutions, peut-être après des milliers de générations. Mais il n'est pas garanti que le modèle produira une solution optimale ou presque optimale.

La raison de la réussite éventuelle du processus repose sur des arguments statistiques plutôt que sur une preuve mathématique exacte. Néanmoins, il y a de solides témoignages expérimentaux selon lesquels, dans de bonnes conditions, le modèle fonctionne pour certains types de problèmes. Voici les principales phases de l'algorithme.

1. Le codage  : Nous précisons d'abord un "code génétique" pour chaque solution potentielle x. Ceci peut se faire en écrivant le nombre x dans la base 2. Par exemple, si x=13, alors son code sera la chaîne binaire 1101 ; si x=65, son code sera 1000001. Le codage binaire est basé sur les puissances de 2. Ainsi, 13, est représenté par la binaire 1101 parceque 1x2³ + 1x2² + 0x2¹ + 1x2⁰ = 8 + 4 + 0 + 1 = 13.

2. La population initiale : Un petit ensemble de chaînes est choisi au hasard dans le pool de solution pour former la population initiale, ou génération o; sur cet ensemble, l'adaptabilité f(x) de chaque x est évaluée. La composition d'une population initiale de six chaînes est donnée ci-dessous.

   

3. Le clonage : Deux chaînes ou plus de la population actuelle sont choisies au hasard pour "s'accoupler". Pour favoriser la reproduction des individus les plus performants, la probabilité qu'une chaîne soit choisie est proportionnelle à son adaptabilité. Dans l'exemple ci-dessus, l'adaptabilité de la chaîne S₂ est deux fois celle de la chaîne S₆. Donc S₂ a deux fois plus de chances que S₆ d'être sélectionnée. Des copies, ou clones, des chaînes sélectionnées sont fabriquées, celles-ci constituant toutes le pool de reproduction.

4. La reproduction : Les chaînes qui s'accouplent disons S₁ et S₂ échangent des segments de gènes consécutifs par croisement pour créer deux enfants ; par exemple il peuvent échanger leurs trois derniers gènes. La longueur et la position des segments permutables sont déterminés par le hasard chaque fois qu'un accouplement a lieu. Dans l'exemple ci-dessous, les chaînes ont échangé leurs gènes 5 à 7.

   

5. La mise à jour de la population : La progéniture qui résulte de l'accouplement remplace soit des chaînes dont l'adaptabilité est faible soit des membres de la population choisis au hasard, selon le schéma particulier de mise à jour. Si nous supposons que les chaînes à remplacer sont S₁ et S₆, alors la composition de la génération suivante est montrée ci-dessous (un procédé de décodage s'applique à chaque chaîne avant le calcul de son adaptabilité) :

   

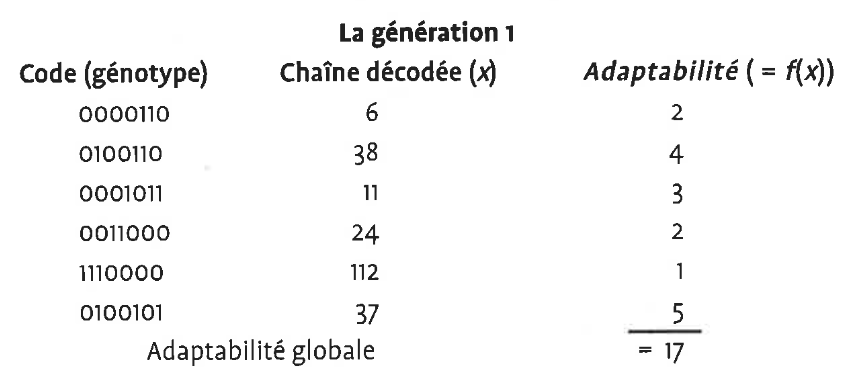
Il est à remarquer que, dans cette nouvelle génération , une solution d'adaptabilité 5 est survenue (x=37), qui est la meilleure jusqu'à présent. Dès lors, l'adaptabilité moyenne de la population est désormais de 2.83 (=17/6), mieux que la moyenne de 2.50 de la génération précédente.

Toutefois, ces améliorations locales après une seule génération ne sont pas significatives et ne fournissent aucune indication comme quoi le modèle marcherait selon l'optique souhaitée. Ce n'est qu'après de multiples générations des étapes 3 à 5 que le procédé produira probablement une chaîne d'adaptabilité supérieure. Nous analyseront plus tard les hypothèses sous-jacentes et les explications possibles des résultats que l'on espère tirer du modèle.

Leçons et questions

Nous allons maintenant révéler la vraie nature de la fonction d'adaptabilité telle que représentée plus haut. Ce qui semble être une fonction arbitraire compte en fait le nombre de fois que les 0 et les 1 alternent dans le code génétique de x.

Plus précisément, l'adaptabilité de x est le nombre d'apparitions des sous-chaînes "01" ou "10" dans la chaîne qui représente x.

Par exemple, f(34) = 4 parceque l'encodage de 34, à savoir 0100100, "01" et "10" apparaissent deux fois chacun.

Donc, la qualité (l'adaptabilité) d'un phénotype x  se reflète de façon directe dans son code génétique.

Or cette situation est assez exceptionnelle en raison de la nature artificielle de notre problème. Dans une application réelle - quand les chaînes encodent des programmes informatiques, par exemple - il n'y a pas de moyen simple pour déterminer quelles combinaisons d'allèles correspondent aux solutions de qualité supérieure. Seuls le temps et le milieu sont en mesure de le dire. Si nous le savions dès le début, nous pourrions alors construire des chaînes optimales tout de suite et il ne serait pas nécessaire de simuler l'évolution. en d'autres termes, la sélection naturelle serait remplacé par le génie génétique.

Dans l'exemple ci-dessus, si nous avions su que plus les 0 et 1 s'entrelacent, meilleures sont les chaînes, nous aurions tout de suite trouvé les chaînes dont l'adaptabilité est optimale en faisant alterner à chaque position : 1010101 (ce qui correspond au phénotype x=85) et 0101010 (x=42).

Même en présence d'un schème de codage favorable, il existe un facteur qui pourrait empêcher le plan de produire une solution optimale : le manque de diversité génétique suffisante.

Le modèle ci-dessus crée de nouvelles combinaisons génétiques par croisement. Mais s'il arrive que toutes les chaînes dans la population initiale ont le même allèle dans une certaine position, ce trait génétique persistera durant toutes les générations futures. Par exemple, si toutes les chaînes du pool initial se terminent par 0, alors aucune quantité de croisement ne parviendra jamais à produire une chaîne se terminant par 1, la solution optimale 1010101 ne pouvant être obtenue. Dans le cas où les deux dernières positions de chaque chaîne initiales sont 0, les deux solutions optimales seront hors de portée de l'évolution. Inspirés de la nature, les algorithmes évolutionnistes, d'une manière générale, comportent aussi un opérateur de mutation pour s'assurer contre la stagnation génétique.

Notre exemple tout simple a illustré les aspects les plus marquants des algorithmes génétiques :

• Le codage. Les solutions potentielles sont représentées par leur "code génétique", sous forme, par exemple, de chaînes binaires.

• Le pool de solutions. Un petit nombre de chaînes forment une "population" de solutions potentielles dont l'algorithme se sert pour cherche de meilleures solutions.

• Le test de performance. La qualité d'une solution est évaluée par un nombre qui représente son "adaptabilité".

• La variation. De nouvelles combinaisons génétiques sont créées, par exemple, par croisement ("reproduction sexuelle").

• La sélection. Ceux qui sont performants ont plus de chances de se reproduire que ceux qui ne le sont pas.

• L'évolution. Les individus nouvellement crées remplacent certaines chaînes du pool de solutions (ou toutes) pour former la prochaine génération.

• Le non déterminisme. Certaines opérations comportent des choix aléatoires ou des règles sur la probabilité.

• La mutation. Des changements locaux aléatoires (mais non fréquents) peuvent se produire dans le code génétique pour accroître la diversité.

Variation, sélection, évolution. Une stratégie séduisante, surtout quand nous faisons face à un problème pour lequel n'est connue aucune méthode efficace de solution. Mais beaucoup de questions subsistent :

• quel est le codage approprié des solutions ?

• comment pouvons-nous mesurer l'adaptabilité ?

• combien de temps mettra une solution optimale ou presque optimale pour apparaître et à quoi la reconnaîtra-t-on ?

• le procédé donnera-t-il le résultat escompté ?

Ce sont là, en effet de très bonnes questions, tellement bonne que la seule réponse honnête que nous puissions donner est que, en général, nous ne savons pas. Ce qui ne signifie pas qu'il n'y a pas de réponses partielles ou même des réponses complètes et très satisfaisantes dans certains cas.

Pour approfondir ce sujet, je ne serais que vous conseiller l'excellent ouvrage d'Arturo Sangalli, Éloge du Flou.

Vous pouvez retrouver le descriptif de ce livre (et de bien d'autres) sur cette page.

Eloge du flou